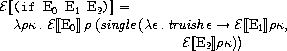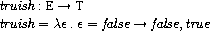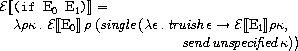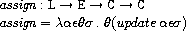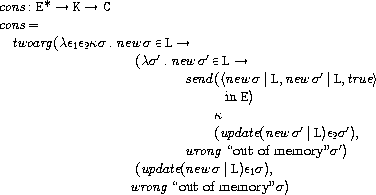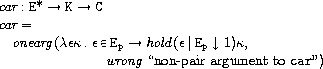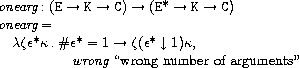きほうのまとめ
いきなりまとめです。
R5RSもそういう流れなんで許してください。

< ... >は列を表します。
一つ目を取り出したり、一つ目を取り除いたものを使ったり、
二つの列を連結させることなどができるため、
実際のところLispのリストと思えば問題ないかと思います。
記法<a, b, c>はLispの(a b c)に対応し、
<>は空リスト()に対応します。
s↓kは列のt番目の要素を表します。
s↓1は(car s)と考えることができます。
#sは列の長さを表します。
(length s)と考えることができます。
s§tは列sと列tの連結を表します。
(append s t)と考えることができます。
s†kは列sから最初のk個の要素を取り除いた列を表します。
s†1は(cdr s)と考えることができます。
t→a,bは"if t then a else b"を表します。
Lispの(if t a b)と考えることができます。
ρ[x/i]は次のような関数を表します。
ρ'(A) = x (A=i)
ρ(A) (otherwise)
つまり、iに対する値がxとなり、それ以外はρのままであるような関数です。
x in DはxのDへの単射です。
多分無視して大丈夫です。
私もよく分かってません。
x | D はxのDへの写像です。
xを集合Dに合う形にします。
詳しくは私も良く分かってません。
 記号の意味がわかったようでわからない……
記号の意味がわかったようでわからない……
 正確な定義とか例とかを知りたいな
正確な定義とか例とかを知りたいな
 調べようと思って参考文献[29]*をAmazonで注文したんだけど、届くのに一ヶ月かかるみたい
調べようと思って参考文献[29]*をAmazonで注文したんだけど、届くのに一ヶ月かかるみたい
 妖精もAmazonを利用しているんだね!
妖精もAmazonを利用しているんだね!
(*)Joseph E. Stoy. Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory. MIT Press, Cambridge, 1977.
らむだきほう
R5RSではこれらの記法の他にラムダ記法というものを用います。
これは、関数fの定義 f(x):=x+1 を λx.(x+1) のように表します。
また、関数fの呼び出しf(2)を (λx.(x+1)) 2 のように表します。
この値はλを取り外しxを2と置き換えることにより
(2+1) = 3 といった風に求められます。
また、 g(x,y) := x+y は λxy.(x+y) と表すことができ、
g(4,5) は (λxy.(x+y)) 4 5 と表すことができます。
ただし、ここで (λxy.(x+y)) 4 は λy.(4+y) となり、
「4と引数を足す関数」になります。
これは、 λxy.(x+y) が実は
λx.λy.(x+y) の略記に過ぎないためです。
ちなみに、このラムダ記法はラムダ計算の記法と似ていますが、
ラムダ計算とは異なるものなのでご注意下さい。
ぶんぽう

まずはプログラムの構文を定義しましょう。
「説明分かりにくすぎ!」
って思うかもしれないけど、R5RSには式があるだけで、
説明なんて一切書いてないのよ♪
こうぶんりょういき
まず、構文領域と呼ばれる記号の列からなる集合を見てみましょう。

Conは 1, #t, 'a, '(b c) のような定数とクォートされたもの全体から成る集合でKはその要素です。
Ideは x, hatena, yousei のような識別子(変数)を全体から成る集合で
Iはその要素です。
Expは (if (eqv? x y) #f (set! y x)) のような一般の式全体から成る集合で
Eはその要素です。
ComはコマンドでExpと同じものでΓはその要素です。
「コマンド」とは副作用のための式で、(lambda () X Y Z) のXとYなどが相当します。
 Γ(ガンマ)と「(かっこ)って似てるわよね
Γ(ガンマ)と「(かっこ)って似てるわよね
 はてなようせい と ひらめきようせい くらいね
はてなようせい と ひらめきようせい くらいね
 呼び捨てにするな! 呼ぶときは"はてなようせいさん"だ!
呼び捨てにするな! 呼ぶときは"はてなようせいさん"だ!
こうぶんきそく
次に、これらの構文規則の要素がどのような記号の列からできているのかを見てみます。
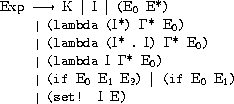
この規則は文脈自由文法を拡張したものを用いて記されています。
式は定数か変数か一つ以上の式を括弧でまとめたものかもしくは……といった内容です。
これらは実際のSchemeの式の一部ですがこの意味論で扱うのはこれだけです。
次に、ConとIdeの生成規則を見てみましょう……といいたいのですが、
なんとR5RSにはExpの生成規則しか書いていません。なんというサボリ!
仕方がないので勝手に想像して書いておきます。正しさは保障しません。
Ide → First Rest*
First → A | B | ... | Z | + | * | ...
Rest → First | 0 | 1 | ... | 9 | ...
Con → Num | #t | #f | 'E
Num → 0 | 1 | ... | 9 | Num Num
ここで出ている数字などはあくまでも文字の列です。
数学的な数とは異なります。
一方、これから定義する意味領域は数学的な数を用います。
 (lambda (I* . I) Γ* E0) において I*が空列の場合どうなるのか分からない
(lambda (I* . I) Γ* E0) において I*が空列の場合どうなるのか分からない
 (lambda ( . x) x) こんな感じになるから構文として正しくないんじゃないかな
(lambda ( . x) x) こんな感じになるから構文として正しくないんじゃないかな
 実はこれは構文として正しいことになってるの。それどころか後でこの形を利用するのよ
実はこれは構文として正しいことになってるの。それどころか後でこの形を利用するのよ
 こんな文法が許されるなんて世も末だね
こんな文法が許されるなんて世も末だね
いみ

ここでもKとかEとかいう記号が出てくるけど、
構文領域のKとEとは全く別物だから注意してね。
Eはエンタープライズ号じゃないからね!
りょういきほうていしき
今度はプログラムの構文に対応する数学的要素を定義します。
一見ただの集合の定義に見えますが、相互再帰的な定義があるため、
通常の集合としては定義できません。
定義するには半順序構造などを使うのでしょうが、
そこら辺は一切書かれていないので触れないことにします。
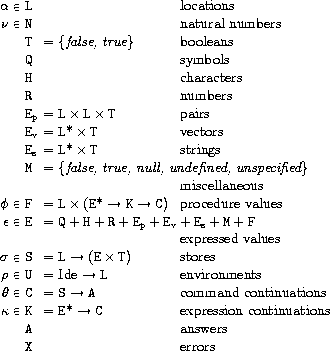
Lはロケーション全体から成る領域です。
ロケーションはメモリのアドレスに相当するものであるので、
自然数などでできていると考えられます。
Nは自然数全体から成る領域です。定義しておきながら実は使いません。
Tはtrueとfalseのみから成る領域です。構文領域の#tと#fがこれに対応します。
Qはシンボル全体から成る領域です。構文領域のIdeがこれに対応します。
Hは文字全体から成る領域です。これもほとんど使いません。
Rは実数全体から成る領域です。これもほとんど使いません。
Epは2つのLとTの組から成るペアを表す領域です。
組の第3要素がtrueの場合そのペアはmutableであり、
falseの場合はimmutableであることを表します。
組は列と同様に扱われます。
EvはLの列とTの組から成るベクタを表す領域です。
組の第2要素はmutable/immutableを表すのでしょうが、
この領域事態自体ほとんど使いません。
EsはEvと同様のものであり、
文字列を表すための領域です。
これもほとんど使いません。
Mは特殊な値を表すための領域です。
Fは(ユーザ定義)関数を表すための領域です。
組の第1要素の値は特に使用しません。
(恐らく関数が保持されるロケーションを表現しているのでしょう。)
細かな内容は後で説明します。
Eは評価済みの値全体から成る領域です。具体的には
シンボル、文字、実数、ペア、ベクタ、文字列、特殊な値、関数です。
 説明長いよ……まだあるの?
説明長いよ……まだあるの?
 まったく。最近の子どもは忍耐力がないわね!
まったく。最近の子どもは忍耐力がないわね!
 わからない……はてなようせいが何歳なのかわからない……
わからない……はてなようせいが何歳なのかわからない……
Sはストア全体から成る領域です。
ストアはロケーションを受け取り、値とフラグの組を返す関数です。
フラグがtrueのときは値が格納済みで、
falseのときは値が格納されていないことを示します。
まさにアドレスを入れたら値を取り出せるメモリの役割を果たしているわけです。
Uは環境全体から成る領域です。
環境は変数を受け取りその値が格納されているロケーションを返す関数です。
つまり、変数の値を取り出すときには、環境とストアの両方を必要とします。
Cはコマンドの継続全体から成る領域です。
コマンドの継続とは「式を評価し終わる直前のもの」のことです。
ストアを与えられることにより評価結果を得られます。
Kは式の継続全体から成る領域です。
式の継続とは「次に評価する式」のことです。
式の継続は前の式の値を受け取ってから評価されます。
受け取るのが値の列なのは多値を受け取る場合もあるためです。
Aは評価結果全体から成る領域です。
とくに何も書かれていないため、ここではEと同様のものとして扱います。
Xはエラーを表す領域です。
実際には有限種類の文字列からできていますが、
あまり深くは触れないことにします。
 結局、領域方程式ってなんだったの?
結局、領域方程式ってなんだったの?
 ググれ!
ググれ!
いみかんすう

そろそろ無駄に長い説明にあきてきたかもしれないけど、
本当に長くなるのはここからよ!
R5RSの形式的意味論は4ページに渡って説明があるけど、
そのうち3ページは意味関数とその補助関数の説明なの。
かんすうのがいよう
構文領域と意味領域の定義が終わったので、
最後にこの二つを対応付ける意味関数を定義します。
定義するのは以下のような関数です。
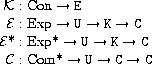
Kは定数を表す文字の並びを意味領域に対応させる関数です。
例えば、数字の並びを数を表す領域R上の対応する数に対応させ、
クォートがついた文字の並びは、クォートを外し、必要があれば
ペアによりリストを構成することにより意味を対応付けます。
R5RSには「Kの定義は面倒だけど面白くないからやらない」とありますので、
ここでもやらないことにします。
Eは式を表す文字の並びを意味領域に対応させる関数です。
Pを評価する式とすると、
EにPを適用することにより
意味を求めることができます(
E[[P]] と表記します)。
この値
E[[P]]をPの意味と呼びます。
ただし、この意味だけでは実際に式を評価したときの値は得られません。
式の値を求めるには以下のようにして環境と式の継続とストアを与える必要があります。
E[[P]]ρ0κ0σ0
ただし、ρ
0は初期環境(組み込み関数の名前とロケーションの対応)、
κ
0は λε
*σ.ε
*
(値の列とストアを受け取り、値の列を返す関数)、
σ
0は初期ストア(組み込み関数のロケーションと実体の対応)です。
κ
0がこのような値なのは意味領域AをEと等しいものと定めているためです。
分かりにくければ領域方程式を見直してみるといいでしょう。
また、変数定義があるプログラムは次のように直されてから評価されます。
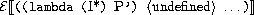
ここでI
*は定義する変数の列、
P'はPの中の定義を代入に直した式、
<undefined>は値undefinedに評価される式です
(変数の初期値として与えられます)。
E*は式(を表す文字の列)の列を受け取り、
対応する値の列を返す関数です。
E同様に環境、式の継続、ストアを受け取る必要があります。
Cは式の列を受け取り、それぞれを評価する関数です。
ただし、その評価によって得られた値は返さず、
一緒に受け取ったコマンドの継続(意味領域Cの要素)をそのまま返します。
詳しくはlambdaと一緒に説明します。
 これでプログラムの意味というものが少しは分かったかしら?
これでプログラムの意味というものが少しは分かったかしら?
 E[[プログラム]]
E[[プログラム]]
ていすうとへんすう
定数に関する評価関数の規則は次のようになっています。
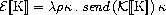
ここで、sendは次のように定義されています。
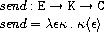
つまり、
Eは定数と環境と式の継続κを受け取ると、
&kappaに定数に対応する意味領域の値εを適用します。
式 1 を評価する場合次のようになります。
E[[1]]ρ0κ0σ0
= (λρκ.send(K[[1]])κ)ρ0κ0σ0
= send(K[[1]])κ0σ0
= (λεκ.κ<ε>)K[[1]]κ0σ0
= κ0<K[[1]]>&sigma0
= (λε*σ.ε*)<K[[1]]>σ0
= <K[[1]]>
意味関数
Kは定数を表す文字の並びを意味領域に対応させるので、
この場合は意味領域Rの要素1を返します。
つまり、1という文字の並びが表現する意味に環境など評価に必要なものを与えると、
1という数が得られるわけです
(正確には1という数のみを含む列ですが、要素数が1の列はその要素自身と同等に扱います。)。
変数に関する評価関数の規則は次のようになっています。
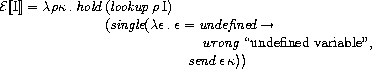
ここで、hold, lookup, singleは次のように定義されています。
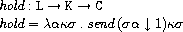
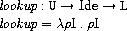
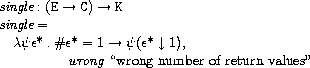
holdはロケーションと式の継続とストアを受け取り、
ストアのロケーションが指し示す値を式の継続に渡します。
lookupは環境と変数を受け取り、変数のロケーションを返します。
singleは要素数が1である値の列のみを受け取る式の継続を作ります。
以上をまとめると、環境から変数に対応するロケーションを取り出し、
それに対応する値を取り出し、
その値が正しければ式の継続に渡すといった処理になります。
式 x を評価する例を示します。
ただし、変数xのロケーションは0であり、その値は100であり、
ρ
1(x)=0, σ
1(0)=<100,true>とします。
E[[x]]ρ1κ0σ1
= hold(lookup ρ1x)
(single(λε.ε=undefined&rarr
wrong "undefined variable",
send εκ0))&sigma1
= send(σ10↓1)(single ...)σ1
= (send 100 κ0) σ1
= 100
よく分からなければ、省略した部分も自分で書いてみると分かるかもしれません。
 わからない……あまりに式の変形が省略されすぎて分からない。
わからない……あまりに式の変形が省略されすぎて分からない。
 わかれ!
わかれ!
 僕ははてなようせいさんのことが分からないよ
僕ははてなようせいさんのことが分からないよ
かんすうてきよう
関数適用に関する規則は次のようになっています。
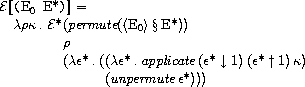
関数適用において「引数の評価順序は決まっていない」というSchemeの規則を再現するために、
permuteという関数で式の列の順序を並び替えてから評価を行い、
unpermuteという関数で得られた値の列の順序を元に戻しています。
この二つの関数は特に定義が与えられていませんが、
permuteで並び替えたものがunpermuteで元の並びに戻る必要があります。
また、applicateは次のように定義されています。

applicateは値を受け取り、その値が関数なら、
関数の第2要素
(関数の領域F=L×(E
*→K→C) であり実体は第2要素がもつ)
に与えられた値の列(引数)と式の継続を渡します。
改めて全体を見てみます。
まず、
E*に関数と引数の列を並び替えたものを渡し、
これを評価したものの列を得ます。
このとき、式の継続として
「値の列を受け取るとそれの並びを元に戻し、
その第1要素(つまり関数)と第1要素を取り除いたもの(つまり引数)と、
本来の式の継続をapplicateに適用する関数」を渡しています。
このため、applicateに送られた関数が正しいものであれば正常に関数適用が行えます。
実際に例を示します。ただし、permuteは列を循環左シフト(<1,2,3>|→<2,3,1>)するもの
unpermuteは列を循環右シフト(<2,3,1>|→<1,2,3>)するものとし、
関数fnは既に定義されているものとします。
E[[(fn 1 2)]]ρκ0σ
= E*(permute(<fn,1,2>) ρ (λ ...))σ
= (&lambda ...) <1,2,E[[fn]]>σ
= applicate(E[[fn]])<1,2>κ0σ
うまくいってそうなのが分かります。
 わからな……
わからな……
 わかれ!
わかれ!
 はてなようせいさん、いまのは"わからないこともない"って言おうとしてたんだよ!
はてなようせいさん、いまのは"わからないこともない"って言おうとしてたんだよ!
かんすうちゅうしょう
関数抽象に関する規則は次のようになっています。

newはストアを受け取り新しいロケーションかエラーを返します。
newはupdateが呼ばれるまでは同じ値を返します。
そのためこの式の中に現れるnewσは全て同じ値です。
また、エラーでないときは
σ(newσ|L)↓2=false
が保障されています。
tievals, extends, updateは次のように定義されています。
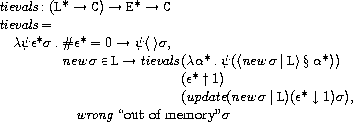
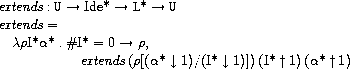
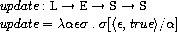
tievalは「ロケーションの列を受け取る関数」と値の列とストアを受け取ると、
受け取った値に新たなロケーションを割り当て、
受け取った関数に新たなロケーションの列を適用します。
extendsは環境と変数の列とロケーションの列を受け取ると、
変数に正しいロケーションを割り当てた新たな環境を返します。
updateはロケーションと値とストアを受け取ると、
ロケーションに値を割り当てた新たなストアを返します。
改めて関数抽象全体を見直してみると、
新たなロケーションを第1要素、
「値の列を受け取りストアを更新し拡張した環境で評価を行う関数」
を第2要素である領域Fの要素を式の継続に適用し
それに関数のロケーションを付け加えたストアを適用します。
関数抽象では
Cという意味関数を使っています。
これは(lambda () X Y Z)のXとYを評価するために使います。
しかし、よく見るとなかなか面白いことになっています。
C[[Γ*]]ρ'(E[[E0]]ρ'κ')
Cは環境とコマンドの継続を受け取ってから評価を始めます。
つまり、
Eによる評価の方が先に行われます。
上の例の場合X, Yより先にZから評価されます。
しかし、
Eにストアが渡されないため、評価は途中で止まります
(この途中の状態がコマンドの継続)。
それからコマンドの列――上の例のX, Yが評価されます。
こちらにはストアが渡されるので順番に評価が行われ、
代入がある場合は変化したストアが最終的にZ(のコマンドの継続)に適用され、
式全体の値が得られます。
関数抽象は分かりにくいと思うのですが、
手順に沿って順番に試すと非常に長くなります。
紙の上などで試す場合、全ステップを書くのではなく、
部分部分試すのをお勧めします。
また、関数適用に関する規則は任意個の引数を持つ関数などの場合も定義されていますが、
固定個の場合と同じ考え方で理解できると思うので説明は割愛させていただきます。
 例がないよ。見たいんだけど
例がないよ。見たいんだけど
 けど、書き出すと長くなるし……
けど、書き出すと長くなるし……
 それではさんすうロボが力をかしてやろう
それではさんすうロボが力をかしてやろう
 いえ、間に合ってます。
いえ、間に合ってます。
いふ
ifに関する規則は次のようになっています。
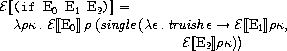
truishはfalseを受け取るとfalseを返し、それ以外を受け取るとtrueを返す関数で、
次のように定義されています。
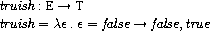
つまり、第1引数を評価し、その式の継続として
「引数が真なら第2引数、偽なら第3引数を評価する関数」を適用しています。
また、引数を二つしか取らないifは次のように定義されています。
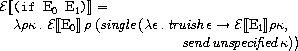
第1引数の値が偽の場合、
sendを使って受け取った式の継続にunspecifiedを適用します。
定義に出てくるunspecifiedはundefined以外の任意の値に変えることが許されています。
 K[[#t]]=true, K[[#f]]=false と定義されているから上手くいくのだ
K[[#t]]=true, K[[#f]]=false と定義されているから上手くいくのだ
 奪われた……私の台詞を奪われた……
奪われた……私の台詞を奪われた……
 謝れ! はてなようせいさんに謝れ!
謝れ! はてなようせいさんに謝れ!
せっとばん
set!に関する規則は次のようになっています。
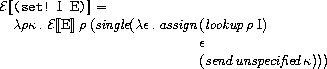
ここで、assignは次のように定義されています。
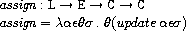
assignはロケーション、値、コマンドの継続、ストアを受け取り、
ストアのロケーションに値を代入した新たなストアをつくり、
そのストアをコマンドの継続に適用します。
定義を良く見れば分かりますが、これは実際にストアに代入を施すより先に
続きの式(式の継続)の評価を始めます。
この評価においてストアが必要となった時点で初めて実際に代入が行われます。
 これで算数もばっちしだね
これで算数もばっちしだね
 何を生意気な……
何を生意気な……
 あんた正直必要ないしそろそろ帰ったら?
あんた正直必要ないしそろそろ帰ったら?
くみこみかんすう
 ここまで読んできた人たちは本当にお疲れ様。
ここまで読んできた人たちは本当にお疲れ様。
それから読み飛ばした人もお疲れ様。
ここまでlambdaやifといった構文を定義してきたけど、
consやcarといった組み込み関数を定義していないわね。
残りはそれだけだから頑張ってね♪
きほん
まず、consとcarの定義を見てみましょう。
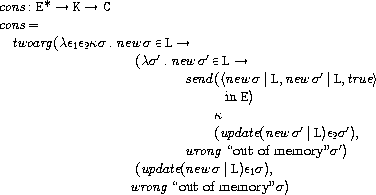
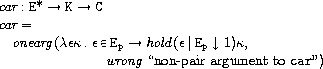
このように全ての組み込み関数は、
E
*→K→C
という型をしています。
ここで意味領域FはL×(E
*→K→C)と定義されているため、
組み込み関数と適当なロケーションとの組は関数となり、
これを初期環境および初期ストアに対応付けることにより
lambdaで定義した関数と同様に使用することができます。
 それでconsとcarの説明は?
それでconsとcarの説明は?
 ございません。財布にもございません。
ございません。財布にもございません。
めんどうなのでしょうりゃく
組み込み関数の定義はけっこうあるのですが、
面倒なので省略させてください。
もう疲れました。
call/ccだけ解説するんでどうかお許し下さい。
 許せ!
許せ!
こ〜るし〜し〜
とりあえず定義を眺めてください。

ここでoneargは次のように定義されています。
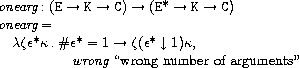
oneargは引数を一つだけとる関数を定義するのに使う関数です。
singleみたいなもんです。
call/cc全体を眺めると、まず引数が1つか確認し、それが関数であれば、
「新たな関数」を作成し、そのロケーションを確保し、
新たなストアの元で受け取った関数に新たな関数を適用しています。
「新たな関数」とは、
「call/ccを呼び出した時点での式の継続に引数を適用する関数」
であり、注意すべきは、式の継続κ'を受け取るにもかかわらず、
それを捨てていることです。
これにより継続オブジェクトを適用した時点までの継続を捨て、
継続オブジェクトの保持する継続に切り替えることができるというわけです。
全てが継続渡しなので非常に分かりやすい定義でいいですね。
 さんすうロボのせいで出番がへってしまった私の悲しさは誰にもわからない……
さんすうロボのせいで出番がへってしまった私の悲しさは誰にもわからない……
 あ、まだいたんだ
あ、まだいたんだ
 そんなのはどうでもいいから、説明して欲しいな
そんなのはどうでもいいから、説明して欲しいな
おわりに
 現実に、負けるな!
現実に、負けるな!
くぬぎたんのふるさとはほくせつ
一応説明しておくと、
クヌギたんとはびんちょうタンのキャラクターです。
北摂とは大阪の北のあたりのことです。
風邪気味でのどが痛いです。
クヌギたんカード欲しさだけに買ったのど飴が役に立っています。
分からないことはググってください。
さいごに
はてなようせい欲しさにやった。
はてなようせいなら何でも良かった。
反省はしていない。
俺がガンダムだ!
「はてなようせいがちーちゃんに見えてきた」という意見があったが、
『○本の住人』なんて知らないぞ!
コミックス持ってたりなんかしないぞ!
さようなら……さようなら……
本当に欲しかったのははてなようせいじゃなくて、
さんすうロボだったのかもしれない……
 わからない……
わからない…… R5RSの形式的意味論を理解した気分になるための冒険は、
R5RSの形式的意味論を理解した気分になるための冒険は、 わからない……
わからない…… R5RSの形式的意味論が理解できた気分になればこんないいことがあるわ。
R5RSの形式的意味論が理解できた気分になればこんないいことがあるわ。
 はてなようせいと学ぶってコンセプトだけど、
はてなようせいと学ぶってコンセプトだけど、
 記号の意味がわかったようでわからない……
記号の意味がわかったようでわからない…… 正確な定義とか例とかを知りたいな
正確な定義とか例とかを知りたいな 調べようと思って参考文献[29]*をAmazonで注文したんだけど、届くのに一ヶ月かかるみたい
調べようと思って参考文献[29]*をAmazonで注文したんだけど、届くのに一ヶ月かかるみたい
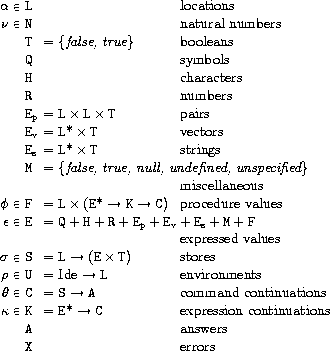
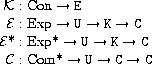
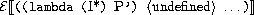
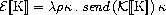
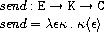
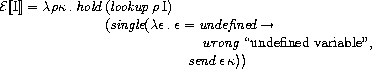
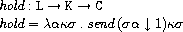
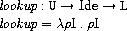
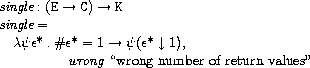
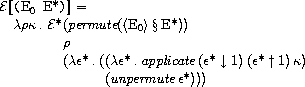


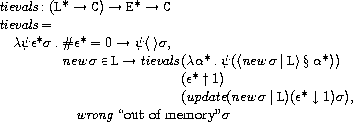
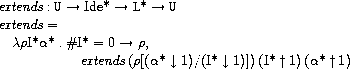
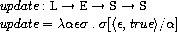
 それではさんすうロボが力をかしてやろう
それではさんすうロボが力をかしてやろう